Where did you get -2 from?
Look at the function again:
(x-2)} )
The graph
cannot be at x=-2 AND x=2.
The point is, at x=2 there is an asymptote, but x=-2 there is no asymptote because it cancels out with the numerator, the only alternative is an open circle.
So whenever you want to find where the open circle is, you take the limit of the function?
To find the y-coordinate of the open circle take the limit of the x value (in this case the x value is -2, so we take the limit of the function to x=-2
We sub it into our original function, just sub in large numbers, and see if they are negative or positive numbers.
For example if I sub in x=1000, and I get the output of y=-0.0000...
Then it approaches positive infinity below the y-axis (because it is a negative y at a very large positive x)
Also, how would you do this question?
1. Shade in the region represented by the following inequalities. Show the coordinates of any axis intercepts and points of intersection in your diagrams.
a)
: x^2-4x+y^2 \leq 0\text{ and } y > 2\sqrt{2}x \right \})
I don't get it :s I know how to find the point of intersection and stuff by using simultaneous equations but I don't know how to graph them or how to even start...
Lets look at our first function, it has an x^2 and a y^2, because we are not doing 4U maths, we can assume that this is a circle graph.
So lets put the circle equation in the form:
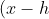^2+(y-k)^2=r^2 )
Where (h,k) is the centre and r radius.
Looking at the equation given to us, lets utilise completing the square in order to get it into a recognisable form:

What do we need to factorise... x because there is an x AND an x^2 there, to get it into its own bracket we must
add 4 to both sides to get a perfect square of x on the LHS

Now we have manipulated our equation to get a perfect square of x:
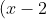^2+y^2=4 )
Here we have the circle equation in a recognisable form
Our centre is (2,0) and radius is 2.
Graph it on the Cartesian axes.
Now for the second graph it is simply a straight line:

It is a line going through the centre of gradient
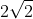
To make graping this straight line easy, just plot (0,0) and the point
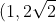 )
(We just sub in x=1 to make plotting easier)
So now we arrive at this, we have a circle and a straight line that intersects it, we arent done yet though, we have inequalities to shade.
Take the circle graph again:
It is:
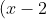^2+y^2 \leq 4 )
The easiest way to know which region to shade, is to pick a point, any point (that DOESNT lie on the curve), and test it.
lets take the point 1,1 and sub it in:
(1-2)^2+1^2=2

Is this true? Yes it is, that means the point (1,1) is valid for this inequality, that means the region which is bounded by the curve that contains (1,1) must be shaded.
Lets do the same for the second inequality, sub in (1,1)

This is INCORRECT, therefore the region that is bounded by the curve that contains (1,1), IS NOT SHADED. We shade the other region, so the other side of the line.
NOTE: Our inequality sign for the SECOND one is >, not
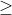
That means we have to make our line dotted to symbolise this inequality.
Now we have two shaded regions, the valid region that is our answer, is the region where they
both overlap. This is the region that is our answer, and you should shade it in a differnet color or something idk.


