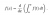liamkk112
Well-Known Member
- Joined
- Mar 26, 2022
- Messages
- 1,065
- Gender
- Female
- HSC
- 2023
yup ur right. idk where i got that its always k^2 lolshouldnt it be k^8 det(A) as when a row/column is multiplied by a scalar k then det(A) increases by a factor of k? so since its an 8x8 matrix it would be k^8?
so final answer is 2162688 i believe then