These as well, please, if anyone could solve these that would be great. I'll be posting more questions up as exams are roughly in a month...


-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to boredofstudies.org!
Students helping students, join us in improving boredofstudies.org by donating and supporting future learners!
- Home
- Forums
- Tertiary Education
- Universities
- University of New South Wales
- Australian School of Business
MATH1251 Questions HELP (5 Viewers)
- Thread starter 1008
- Start date
These as well, please, if anyone could solve these that would be great. I'll be posting more questions up as exams are roughly in a month...


Thanks! I've got a few more...



EDIT: Figured out two, I've deleted those from here
Last edited:
Thanks! I've got a few more...



EDIT: Figured out two, I've deleted those from here
http://hyperphysics.phy-astr.gsu.edu/hbase/oscda.html#c1 .)
Last edited:
Thanks for that, I'll figure (3) out now too... Got another one, from series this time, I'm completely stuck:

Also, is this correct?

Last edited:
a) Actually follows immediately from the p-series test (here, it's summing 1/n^p, where p = 1/2 < 1 ==> divergence).Thanks for that, I'll figure (3) out now too... Got another one, from series this time, I'm completely stuck:

Last edited:
Part b) is a famous elementary proof of the Harmonic series' divergence:
S = 1 + (1/2 + 1/3) + (1/4 + 1/5 + 1/6 + 1/7) + (1/8 + 1/9 + 1/10 + 1/11 + 1/12 + 1/13 + 1/14 + 1/15) + ...
> 1 + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) + (1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16) + ...
= 1 + 1/2 + 1/2 + 1/2 + ...
= ∞,
so the Harmonic series diverges.
Edit: Just realised the Q. wanted a different bracketing to the one I did here. But it's the same idea, and you should be able to do it their way if you understand what was done here.
S = 1 + (1/2 + 1/3) + (1/4 + 1/5 + 1/6 + 1/7) + (1/8 + 1/9 + 1/10 + 1/11 + 1/12 + 1/13 + 1/14 + 1/15) + ...
> 1 + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) + (1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16) + ...
= 1 + 1/2 + 1/2 + 1/2 + ...
= ∞,
so the Harmonic series diverges.
Edit: Just realised the Q. wanted a different bracketing to the one I did here. But it's the same idea, and you should be able to do it their way if you understand what was done here.
Last edited:
Paradoxica
-insert title here-
Alternatively, using the simple fact that

The sum is reduced to a telescopic inequality, and it is trivial to obtain:
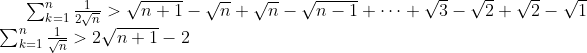
And so the infinite sum clearly diverges.
The sum is reduced to a telescopic inequality, and it is trivial to obtain:
And so the infinite sum clearly diverges.
Paradoxica
-insert title here-
Both sides are the same.
Thanks IG, leehuan and Paradoxica:
leehuan, how'd you get rid of the equality in this one?:
Also, is this correct?

leehuan, how'd you get rid of the equality in this one?:
I think I did a) like this
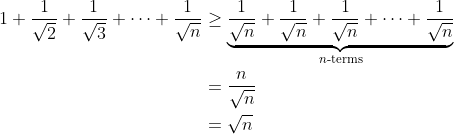
Also, is this correct?

leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Oh lol I see now, whoops.Both sides are the same.
Yeah your /img is right. We did that one in my tutorial. Just compare.Thanks IG, leehuan and Paradoxica:
leehuan, how'd you get rid of the equality in this one?:
Also, is this correct?

Technically they aren't equal and I should've just used > and not \ge
Paradoxica
-insert title here-
if at least one term in the inequality sum isn't equal, then it's unequal. FTFY.Oh lol I see now, whoops.
Yeah your /img is right. We did that one in my tutorial. Just compare.
they aren't equal and I should've just used > and not \ge
note the same holds true for integrals, if two functions are equal at a finite number of points, then provides one is larger than the other over the domain of integration, the integrals are not equal.
Thanks IG, leehuan and Paradoxica:
leehuan, how'd you get rid of the equality in this one?:
Also, is this correct?

leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Oh yeah, in the question book they said it was safe to assume that the sequences are non-negative. I think he just forgot to mention that.
I don't think it says it's safe to assume that for this question.... Here's the proper screenshot:Oh yeah, in the question book they said it was safe to assume that the sequences are non-negative. I think he just forgot to mention that.

Paradoxica
-insert title here-
are you sure the n is independent of the a_n? I read the n as depending on the index.

