Also, neither the Itute nor TL solns provided a satisfactory explanation for why the negative
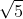
solution was invalid in Q14c(ii).
} = \sqrt{\frac{5 \pm \sqrt{5}}{8} })
Itute gave no reasoning for selection of the +ive inner surd, while TL reasoned that cos^2() must be positive (but clearly the [
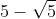
] solution is also positive).
My reasoning is that where we subst,
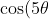 = \cos(\pi/2) = 0)
,
in order to get the polynomial, we could equally well have substituted
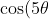 = \cos(3\pi/2) = 0)
,
to get the same equation.
So the polynomial is equally valid for solving for,
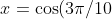)
, as well as some other non acute angles (which clearly can be ignored).
So the two acute solutions,
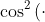} = \sqrt{\frac{5 \pm \sqrt{5}}{8} })
correspond to solutions for cos(pi/10) and cos(3pi/10), and since cos() is a decreasing function on (0,pi), then the larger value must correspond to cos(pi/10).
Did anyone else use this reasoning?

