The value of the sample variance is the spread of the data
within the sample. It will always vary depending on what sample you get. It is a realisation of an experiment so it shouldn't really have any probabilities in it. In your example, say you take a sample of 100 pens out of 1000 pens and see how many are faulty. It doesn't make sense that in
every sample of 100 pens you will get exactly 10 pens that are faulty. You may get 9 or 12 pens etc as it depends on your sample.
Perhaps worth looking at this from first principles. Let
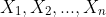
each be Bernoulli trials. Denote
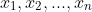
as the realisation (or data points) of each of these random variables. These are just a bunch of 0s and 1s where 0 represents failure and 1 represents success.
Suppose that out of the n trials, we get m successes (m<n) which is our
particular sample. This means that our sample data has m lots of 1s and n-m lots of 0s so
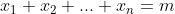
hence the sample mean is simply
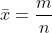
The sample variance is given by
^2)
After some algebra simplifying you get
}{n^2(n-1)})
which means that
}{n-1})
Notice that your sample mean is in fact your sample proportion. At no point did we use the probability of success in the context of the sample but rather the relative frequency in the sample.
This is different to the variance of the
random variable which uses probabilities and distribution functions to measure its spread. This is what most questions typically ask about.
