A curve isn't differentiable at a point if it satisfies either of two conditions:
1. Its not continuous at that point (i.e. its not defined there)
2. Has a cusp (a steep point in a graph)
A classic example of a curve with a cusp is
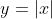
which isn't differentiable at x=0. Any curve having a discountinity isn't differentiable at that point. Now if you want a function that isn't differentiable anywhere yet is continuous:
https://en.wikipedia.org/wiki/Weierstrass_function