-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Optimisation? (1 Viewer)
- Thread starter mmmm.
- Start date
#RoadTo31Atar
Well-Known Member
- Joined
- Oct 11, 2019
- Messages
- 322
- Gender
- Undisclosed
- HSC
- 2020
I would think of it like this
1. Read question while simultaneously writing down all the useful info they give you
2. From that info and the question think of what they want you to find
3. Write down formulas which be used (this is important even if it's like a rectangle because these questions can get very confusing)
4. From the info you wrote in step 1 you can now make some substitutions if ur formulas are good, if u can't you need to go back and think of more/better formulas
5. Usually you'll write everything in terms of x or whatever and differentiate or whatever they want from you
You might need to sub something into the original equation or show proof that it's a min or max point which you can also do very easily (very important to show that it is a max or min point, I think you can lose a mark here if u don't do this even if it's only 1 point and ur answer is right)
Sometimes you need to use Pythagoras or find shapes, I would recommend drawing diagrams for this.
I would do these questions last in an exam because they kinda suck and take a bit of effort if you can't figure it out right away.
1. Read question while simultaneously writing down all the useful info they give you
2. From that info and the question think of what they want you to find
3. Write down formulas which be used (this is important even if it's like a rectangle because these questions can get very confusing)
4. From the info you wrote in step 1 you can now make some substitutions if ur formulas are good, if u can't you need to go back and think of more/better formulas
5. Usually you'll write everything in terms of x or whatever and differentiate or whatever they want from you
You might need to sub something into the original equation or show proof that it's a min or max point which you can also do very easily (very important to show that it is a max or min point, I think you can lose a mark here if u don't do this even if it's only 1 point and ur answer is right)
Sometimes you need to use Pythagoras or find shapes, I would recommend drawing diagrams for this.
I would do these questions last in an exam because they kinda suck and take a bit of effort if you can't figure it out right away.
Mainly just know how to differentiate. Make sure you are able to solve word-problems e.g. maximising area enclosed by a fence, maximise the volume of a cardboard box etc.
Make sure to communicate your working out correctly.
Make sure you know to determine the concavity of a curve using the second derivative. e.g. x^3 - 1
There are probably are some youtube videos if you need.
Make sure to communicate your working out correctly.
Make sure you know to determine the concavity of a curve using the second derivative. e.g. x^3 - 1
There are probably are some youtube videos if you need.
B1andB2
oui oui baguette
KEEP AN EYE OUT FOR SIMILARITY
and make sure you understand what you are finding because there is one hard question in which no stationary point exists and you need to understand the limit
and make sure you understand what you are finding because there is one hard question in which no stationary point exists and you need to understand the limit
Another piece of advice for optimisation and max/min problems: If you get stuck, try going back to the question and looking for any piece of information that you have not used. It is unusual for questions in maths exams to provide information that is not needed, so if you are stuck and there is something that you have not used, that could be why you are stuck.
Example: A metal can is to be made in the shape of a cylinder with sealed ends. Find the value of r:h, the ratio of the radius of the cylinder (r cm) to its height (h cm) that minimises the amount of metal used to make a can of fixed total volume V cm3.
Solution: Let A cm2 be the surface area of the can, and so
})
Minimising the amount of metal used means minimising A, but we can't do calculus on the above equation with three variables.
Looking back at the question, the piece of information that is unused is that the can has a fixed total volume V.
})
and so we can form an equation in two variables (V is a constant) by putting (2) into (1) and then use calculus:
: } h &= \frac{V}{\pi r^2} \\ \frac{r}{h} &= r \times \frac{\pi r^2}{V} = \frac{\pi r^3}{V} \\ \\ \text{So, when } r^3=\frac{V}{2\pi},\ \frac{r}{h} &= \frac{\pi}{V} \times \frac{V}{2\pi} = \frac{1}{2} \\ \\ \text{So, the amount of metal is minimised when } r:h &= 1:2 \end{align*})
Example: A metal can is to be made in the shape of a cylinder with sealed ends. Find the value of r:h, the ratio of the radius of the cylinder (r cm) to its height (h cm) that minimises the amount of metal used to make a can of fixed total volume V cm3.
Solution: Let A cm2 be the surface area of the can, and so
Minimising the amount of metal used means minimising A, but we can't do calculus on the above equation with three variables.
Looking back at the question, the piece of information that is unused is that the can has a fixed total volume V.
and so we can form an equation in two variables (V is a constant) by putting (2) into (1) and then use calculus:
It is worth noting, in my opinion, that my optimisation example illustrates a general exam strategy that I believe is under-utilised, which is:
Keep your eye on your goal.
In this question, my goal was the ratio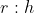
, and while that can be found by finding 
and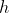 
and then dividing them, I am not actually required to find or .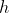
In forming equation (2), I recognised that I was planning to use it to eliminate or 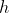from equation (1). Thus, I expressed (2) in the form that suited simplifying (1), rather than making 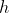the subject and adding an extra line of algebra into the substitution step to get to the equation linking 
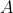to .
As I showed later, rearranging equation (2) gave me a form for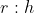 where the only variable present was 
.
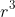Thus, I worked with the stationary point being at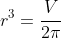
. I knew that I could take the cube root if I needed but recognised also that knowing 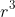was likely to be sufficient. This also told me that using equation (2) to back-substitute and find an exact form for 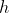was likely to be unnecessary.
In other words, I didn't stop to find an explicit form for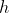 or as neither of them was my goal.
In doing so, I avoided:
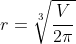
^2 = \sqrt[3]{\frac{V^3}{\pi^3} \times \frac{4\pi^2}{V^2}} = \sqrt[3]{\frac{4V}{\pi}})
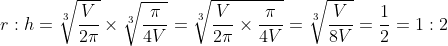
This is a strategy that can save you time and possibly also avoid losing marks from mistakes in working that isn't actually needed anyway.
Keep your eye on your goal.
In this question, my goal was the ratio
In forming equation (2), I recognised that I was planning to use it to eliminate
As I showed later, rearranging equation (2) gave me a form for
Thus, I worked with the stationary point being at
In other words, I didn't stop to find an explicit form for
In doing so, I avoided:
This is a strategy that can save you time and possibly also avoid losing marks from mistakes in working that isn't actually needed anyway.