Intilegience
New Member
- Joined
- Dec 18, 2023
- Messages
- 12
- Gender
- Male
- HSC
- 2024
Hey, I've been stuck on this question for a while so was hoping if someone could help me with parts c and d. (parts a and b given for context)
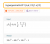
a) obtain cos6θ as a polynomial in cosθ.
b) Hence show that x=cos ((2k+1) π)/12 where k=0,1,2,3,4,5 are the roots of the equation 32x^6-48x^4+18x^2-1=0
c)deduce that cos π/12 * cos5π/12=1/4
d) deduce that cos^2 5π/12 +cos^2 π/12=1
I also would like some advice on how to tackle these types of problems better, right now my approach is to just haphazardly use sum and product of roots to try to get a relationship, but If someone could maybe give some tips on how to approach these types of questions better, I would really appreciate it.
a) obtain cos6θ as a polynomial in cosθ.
b) Hence show that x=cos ((2k+1) π)/12 where k=0,1,2,3,4,5 are the roots of the equation 32x^6-48x^4+18x^2-1=0
c)deduce that cos π/12 * cos5π/12=1/4
d) deduce that cos^2 5π/12 +cos^2 π/12=1
I also would like some advice on how to tackle these types of problems better, right now my approach is to just haphazardly use sum and product of roots to try to get a relationship, but If someone could maybe give some tips on how to approach these types of questions better, I would really appreciate it.
Last edited: