-
Looking for HSC notes and resources? Check out our Notes & Resources page
Polynomials (1 Viewer)
- Thread starter Lukybear
- Start date
pwoh
O_O
a and b are just arbitrary constants right?
Btw I have no idea, I hope someone answers this..
Btw I have no idea, I hope someone answers this..
- Joined
- Feb 16, 2005
- Messages
- 8,405
- Gender
- Male
- HSC
- 2006
If w is a complex root of a cubic polynomial of unity (x3 - 1 = 0) then so is 1 and w2 i.e. the polynomial has roots 1, w and w2. It might make it easier to picture by calling them α, β and γ which means you want an equation with roots (aα + b)-1, (aβ + b)-1 and (aγ + b)-1 which is now a standard problem of forming polynomial equations.If w is a compelx cube root of 1, form a cubic with root (a+b)^-1, (aw+b)^-1, (aw^2 + b)^-1
Let y = (ax + b)-1, make x the subject and sub it into the polynomial equation.
omgmynameislong
Member
- Joined
- Dec 20, 2008
- Messages
- 207
- Gender
- Male
- HSC
- 2010
sub in w and then sub in 1/w. For the 1/w equation times the whole thing by w^8 then ull get the same equation.
Last edited:
P(z)=(z^4-5/4)^2-(3/4)^2And also prove that
if w is a root of P(z) = z^8-5/2z^4+1
then 1/w is also a root
Also find one of the roots of P(z)=0 in exact form
=(z^4-2)(z^4-1/2)
For roots to be in GS:
Let roots be; A/r,A,Ar.
And you'll get A=cbrt(-d/a) [Using sum of roots]
If this is not enough;
r+r^-1=b^3/(a^2.d)-1 [Using prod and sum of roots]
And; A=sqrt((adc/(b^3-a^2.d)))
And; A=-b/c [Using sum of roots twice and sum of roots]
This question seems pretty vague but the conditions above (if they're correct) are probs enough unless they're asking for a Geometric argument.
Last edited:
What about this: Find the conditions for the roots of the cubic equation ax^3 + bx^2 +cx + d = 0 to be in geometric sequence
Let roots be
Using product of roots...
Subbing it back into the equation, as a is a root
Then cubing
Hopefully that's right.
Isn't it quicker for this equation to prove 1/w = conjugate(w)And also prove that
if w is a root of P(z) = z^8-5/2z^4+1
then 1/w is also a root
Also find one of the roots of P(z)=0 in exact form
Then use the fact that a poly with real coefficients has roots occuring in conjugate pairs?
The only problem is that 1/w = conjugate(w) only when |w| = 1.Isn't it quicker for this equation to prove 1/w = conjugate(w)
Then use the fact that a poly with real coefficients has roots occuring in conjugate pairs?
So that doesn't work
Minor detail: since (w =/= 0)sub in w and then sub in 1/w. For the 1/w equation times the whole thing by w^8 then ull get the same equation.
Last edited:
Oh yeah.The only problem is that 1/w = conjugate(w) only when |w| = 1.
So that doesn't work
...
I knew that, I was just testing that everyone else knew that.
MetroMattums
Member
- Joined
- Apr 29, 2009
- Messages
- 233
- Gender
- Male
- HSC
- 2010
Nvm. Need to rethink this.
Last edited:
How do u know w^8 =1?sub in w and then sub in 1/w. For the 1/w equation times the whole thing by w^8 then ull get the same equation.
For this one, what do we do from here?P(z)=(z^4-5/4)^2-(3/4)^2
=(z^4-2)(z^4-1/2)
sorry for idiocy.
any1?How do u know w^8 =1?
Well, confirming 1/w is easy.For this one, what do we do from here?
sorry for idiocy.
P(x)=(z^4-2)(z^4-1/2)
=(z^2-sqrt(2))(z^2+sqrt(2))(z^2-1/sqrt(2))(z^2+1/sqrt(2))
From here roots are:
z=+-2^(1/4),+-2^(-1/4),+-i.2^(1/4),+-i.2^(-1/4).
Well, you've found complex roots;Sorry shaon0, could you just expand on how to confirm 1/w. Im thinking to do that question w^8 =1. But w is not a root of unity, but a root of p(z).
nd thxs for the roots bit. Ive got that.
Say, w=+-i(2)^(1/4), 1/w=1/(+-i.2^(1/4))=-+i.2^(-1/4) (as listed)
Try prod. of roots and sum.
Last edited:
MetroMattums
Member
- Joined
- Apr 29, 2009
- Messages
- 233
- Gender
- Male
- HSC
- 2010
Sub 1/w in the equation, then take (1/w)^8 out of it, then you get the original equation, which is equal to 0. Hence, 1/w is a root.
=w^{8}-\frac{5}{2}w^{4}+1=0)
=(\frac{1}{w})^{8}-\frac{5}{2}(\frac{1}{w})^{4}+1 =(\frac{1}{w})^{8}(1-\frac{5}{2}w^{4}+w^{8})=(\frac{1}{w})^{8}(0)=0)
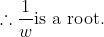
For the first first first post, let x be a root of x^3 - 1 = 0 then let the roots of the new equation have a general form y = 1/(ax+b). Then, get those roots in terms of x then sub it into x^3 - 1 = 0. You should get the equation.
For the first first first post, let x be a root of x^3 - 1 = 0 then let the roots of the new equation have a general form y = 1/(ax+b). Then, get those roots in terms of x then sub it into x^3 - 1 = 0. You should get the equation.
Last edited:
