By definition, isn't an inverse function:
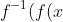)=x)
So sin inverse of sin 1=1
and sin inverse of sin 1.5=1.5
BUT, sin inverse of sin 2=pi-2
and sin inverse of sin3=pi-3
And even to the extent that: sin inverse of sin 100=100-32pi.
Noting that everything is in radians. Can someone explain this?
So sin inverse of sin 1=1
and sin inverse of sin 1.5=1.5
BUT, sin inverse of sin 2=pi-2
and sin inverse of sin3=pi-3
And even to the extent that: sin inverse of sin 100=100-32pi.
Noting that everything is in radians. Can someone explain this?
