member 6003
Member
- Joined
- Apr 20, 2022
- Messages
- 83
- Gender
- Male
- HSC
- 2023
you have to start with this:
where z, w are any complex numbers

And prove:

My method:
let Z,W be conjugates of z,w

 - expand RHS
- expand RHS

then if the thing is true then:

square both sides:

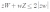
and then I'm stuck. I saw another guy do the question on stack exchange and they basically got to the same step but then squared both sides again (letting z=a+ib, w=x+iy) and whatever, then factorise so that its like x^2>=0 therefore must be true.
But I don't understand how you can square both sides at this step since LHS can be negative, and RHS must be positive. I thought you could only square both sides of an inequality when both sides are positive.
This question is out of extension 2 Cambridge 1D question Q25 b)
where z, w are any complex numbers

And prove:

My method:
let Z,W be conjugates of z,w

 - expand RHS
- expand RHS
then if the thing is true then:

square both sides:

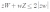
and then I'm stuck. I saw another guy do the question on stack exchange and they basically got to the same step but then squared both sides again (letting z=a+ib, w=x+iy) and whatever, then factorise so that its like x^2>=0 therefore must be true.
But I don't understand how you can square both sides at this step since LHS can be negative, and RHS must be positive. I thought you could only square both sides of an inequality when both sides are positive.
This question is out of extension 2 Cambridge 1D question Q25 b)
Attachments
-
7.6 KB Views: 5
-
5.6 KB Views: 5


