-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Q10 James Ruse Ext 1 2022 (1 Viewer)
- Thread starter Anaya R
- Start date
Would the following information help?
For to have only one asymptote, the discriminant of
to have only one asymptote, the discriminant of 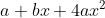 must be a negative value.
must be a negative value.
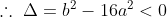
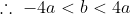
Since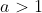 ,
, 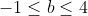 satisfies the requirement
satisfies the requirement  .
.
The answer is therefore C.
For
Since
The answer is therefore C.
Anaya R
Well-Known Member
Because it’s a reciprocal function, there’s by default gonna be an asymptote where y=0. Therefore, there must be no other asymptotes, which means that there are no real x values for which the polynomial on the denominator is =0. Hence, the discriminant for the denominator must be less than (not equal to) 0. Rearranging,
0>b^2-4ac
0>b^2-16a^2
b^2<16a^2
therefore -4a<b<4a
So therefore, A, B and D don't work. But, because a>1, technically we can also say that
-4<=b<=4
and -1<=b<=4 is within that domain, so it is also true.
0>b^2-4ac
0>b^2-16a^2
b^2<16a^2
therefore -4a<b<4a
So therefore, A, B and D don't work. But, because a>1, technically we can also say that
-4<=b<=4
and -1<=b<=4 is within that domain, so it is also true.
damnit my wifi went out and i didnt see ur reply before i posted mine lolWould the following information help?
Forto have only one asymptote, the discriminant of
must be a negative value.
Since,
satisfies the requirement
.
The answer is therefore C.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
For the denominator
But if it is a post MC question the complete answer is

