stickyricebuns
Member
- Joined
- Apr 25, 2020
- Messages
- 48
- Gender
- Female
- HSC
- 2021
hi
1. for this equation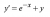 the question asks, "based on the slope field, determine the behaviour of y as x approaches infinity". the answer is y approaches plus minus infinity and 0
the question asks, "based on the slope field, determine the behaviour of y as x approaches infinity". the answer is y approaches plus minus infinity and 0
i'm confused how to find the limits from the slope field? i've drawn it and it just looks like this: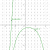 but how do you get y approaches 0 and infinity?? i'm unsure if the solution graph on the left (goes straight up) is the reason for y approaching infinity. because as x approaches infinity, at some point it still has to come back down before x is really "at infinity" no?
but how do you get y approaches 0 and infinity?? i'm unsure if the solution graph on the left (goes straight up) is the reason for y approaching infinity. because as x approaches infinity, at some point it still has to come back down before x is really "at infinity" no?
for y=0 i asked someone and they explained that the reason y approaches 0 is because when y'=0, y=-e^-x. so along the exponential curve the gradient is 0, so as x approaches 0, y also approaches 0. i only understand it a little so can someone pls explain it more in depth.
2. for this equation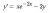 it asks the same thing ("draw slope field, find lim x->inf) (answer is 0)
it asks the same thing ("draw slope field, find lim x->inf) (answer is 0)
how do you draw the slope field in the first place ?? my understanding is letting y'=m so you get an equation in terms of y, x and m (y= x/2 * e^-2x - m) then sub in values of m and draw the slopes.
this seems kind of ?? like ?? really tedious? because the graph that u have the draw the slopes across isn't something that's intuitive so u have to take time to draw what it looks like before transforming it and doing the slope field. so is there a diff way to graph this slope field that isn't super time consuming.
i did ask the teacher and they said to "let x=1" and just graph y'=e^-2-2y. but why is this a valid way of drawing the slope graph bc x is a variable and you're just making it a constant so you're overall changing the equation from the question hence not answering the question at all. i put it into geogebra and it also doesn't approach 0 (instead approaching something like 0.1) so like. wat
thank u
1. for this equation
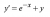 the question asks, "based on the slope field, determine the behaviour of y as x approaches infinity". the answer is y approaches plus minus infinity and 0
the question asks, "based on the slope field, determine the behaviour of y as x approaches infinity". the answer is y approaches plus minus infinity and 0i'm confused how to find the limits from the slope field? i've drawn it and it just looks like this:
 but how do you get y approaches 0 and infinity?? i'm unsure if the solution graph on the left (goes straight up) is the reason for y approaching infinity. because as x approaches infinity, at some point it still has to come back down before x is really "at infinity" no?
but how do you get y approaches 0 and infinity?? i'm unsure if the solution graph on the left (goes straight up) is the reason for y approaching infinity. because as x approaches infinity, at some point it still has to come back down before x is really "at infinity" no?for y=0 i asked someone and they explained that the reason y approaches 0 is because when y'=0, y=-e^-x. so along the exponential curve the gradient is 0, so as x approaches 0, y also approaches 0. i only understand it a little so can someone pls explain it more in depth.
2. for this equation
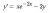 it asks the same thing ("draw slope field, find lim x->inf) (answer is 0)
it asks the same thing ("draw slope field, find lim x->inf) (answer is 0)how do you draw the slope field in the first place ?? my understanding is letting y'=m so you get an equation in terms of y, x and m (y= x/2 * e^-2x - m) then sub in values of m and draw the slopes.
this seems kind of ?? like ?? really tedious? because the graph that u have the draw the slopes across isn't something that's intuitive so u have to take time to draw what it looks like before transforming it and doing the slope field. so is there a diff way to graph this slope field that isn't super time consuming.
i did ask the teacher and they said to "let x=1" and just graph y'=e^-2-2y. but why is this a valid way of drawing the slope graph bc x is a variable and you're just making it a constant so you're overall changing the equation from the question hence not answering the question at all. i put it into geogebra and it also doesn't approach 0 (instead approaching something like 0.1) so like. wat
thank u
