I did inverse tan(-1/Root3) and that gave me -30 but none of the answers were related to -30.
The reason that none of the answers is -30º is that the inverse tan function always returns angles between -90º and +90º, since the tan function is restricted to the domain -90º < x < 90º to make it have an inverse, because if we didn't restrict the domain, the function wouldn't be invertible, as it isn't one-to-one otherwise. (This is taught in the 3U course.)
So the -30º you got is the unique angle
x in the domain -90º ≤ x ≤ 90º that makes tan
x equal -1/√3. Note that in each "branch" of the tan function (see the graph of it:
http://www.analyzemath.com/trigonometry/graph_tangent.gif; each branch is a domain of the form
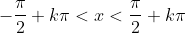
, for
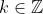
(integers)), there will be exactly one angle (x-value) that makes the tan function take on a given value (in our case -1/√3). We want angles that fall between 0 and 360º. Since the tan function has a period of
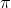
(that is, it repeats its value every time you increase/decrease the x-value by
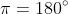
), if we know one solution, we know that any multiple of 180º added to this solution is also a solution. Since we know one solution is -30º, we know the following are also solutions:
-30º±180º, -30º±2•(180º), -30±3•(180º), and so on.
Only two of these will fall between 0 and 180º, so we only select those ones since we are only asked to find the solutions in this particular interval.





