Can you clarify what aspect(s) of question 4 are troubling you?
The question, IMO, reads as being much broader than I think is intended. The requirement that "
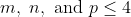
" covers not only the cases where they are positive integers (which is what I suspect was intended) but extends to rational values and negative values, making the investigation much broader. Rational powers can produce roots with vertical tangents. Negative powers will lead to vertical asymptotes. Non-integer powers can also lead to a non-continuous domain.
My advice is to take
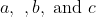
as small, non-zero integers and to take
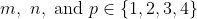
. Then, the graph of
)
will be the graph of a polynomial with roots at
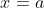
,
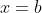
, and
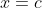
. Your investigations / experiments with different values should show:
- When the power
 is 1, the root at
is 1, the root at  will be a single root.
will be a single root.
- The graph of
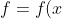) will simply crossing the
will simply crossing the  -axis at
-axis at  .
.
- The sign of
) can be changing from positive to negative or negative to positive, and so will resemble one of the roots of a parabola which crosses the
can be changing from positive to negative or negative to positive, and so will resemble one of the roots of a parabola which crosses the  -axis twice.
-axis twice.
- To be more precise, the appearance of the root will match that of a parabola with the corresponding sign change and where the concavity of the parabola (up or down) matches that of the root of
) in the vicinity of
in the vicinity of 
- That is, if
) is concave up near
is concave up near  , a single root will resemble a parabola like
, a single root will resemble a parabola like 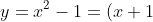(x-1)) looks near its roots... depending on the sign change of the graph of
looks near its roots... depending on the sign change of the graph of ) , it will be similar in appearance near
, it will be similar in appearance near  to the parabola
to the parabola 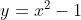 near either
near either 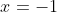 or
or 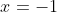 .
.
- If
) is concave down near
is concave down near  , a single root will resemble a concave down parabola like
, a single root will resemble a concave down parabola like 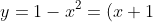(1-x)) looks near its roots... depending on the sign change of the graph of
looks near its roots... depending on the sign change of the graph of ) , it will be similar in appearance near
, it will be similar in appearance near  to the parabola
to the parabola 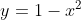 near either
near either 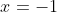 or
or 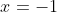 .
.
- When the power
 is 2, the root at
is 2, the root at  will be a double root.
will be a double root.
- The graph of
) will touch but not crossing the
will touch but not crossing the  -axis.
-axis.
- The
 -axis will be a tangent to the curve
-axis will be a tangent to the curve ) at the point
at the point ) .
.
- The sign of
) will not change: it will either be positive both before and after
will not change: it will either be positive both before and after  and zero at
and zero at  , or be negative both before and after
, or be negative both before and after  and zero at
and zero at  .
.
- In the region around
 , the curve
, the curve ) will resemble either
will resemble either 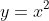 or
or 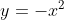 near their double roots at the origin.
near their double roots at the origin.
- Which of these two parabolas
) resembles can be determined either by considering the concavity at
resembles can be determined either by considering the concavity at  (concave up resembles
(concave up resembles 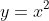 , whereas concave down resembles
, whereas concave down resembles 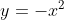 ) or by looking at the sign of
) or by looking at the sign of ) around the root (if
around the root (if ) follows the pattern negative - zero - negative around
follows the pattern negative - zero - negative around  , it resembles
, it resembles 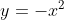 ; if
; if ) follows the pattern positive - zero - positive around
follows the pattern positive - zero - positive around  , it resembles
, it resembles 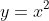 )
)
- When the power
 is 3, the root at
is 3, the root at  will be a triple root.
will be a triple root.
- The graph of
) will have the
will have the  -axis as a tangent at
-axis as a tangent at  and it will cross the
and it will cross the  -axis.
-axis.
- The point
) will be a horizontal point of inflection on the curve
will be a horizontal point of inflection on the curve ) .
.
- The sign of
) will change around
will change around  .
.
- In the region around
 , the curve
, the curve ) will resemble either
will resemble either 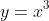 or
or 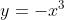 in the region around the origin.
in the region around the origin.
- Which cubic
) resembles can be determined either by examining the sign change around
resembles can be determined either by examining the sign change around  , or by looking at the concavity change: negative and concave down - zero - positive and concave up will resemble
, or by looking at the concavity change: negative and concave down - zero - positive and concave up will resemble 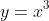 ; positive and concave up - zero - negative and concave down will resemble
; positive and concave up - zero - negative and concave down will resemble 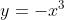 .
.
- When the power
 is 4, the root at
is 4, the root at  will be a quadruple root.
will be a quadruple root.
- The graph of
) will touch but not crossing the
will touch but not crossing the  -axis.
-axis.
- The
 -axis will be a tangent to the curve
-axis will be a tangent to the curve ) at the point
at the point ) .
.
- The sign of
) will not change: it will either be positive both before and after
will not change: it will either be positive both before and after  and zero at
and zero at  , or be negative both before and after
, or be negative both before and after  and zero at
and zero at  .
.
- In the region around
 , the curve
, the curve ) will resemble either
will resemble either 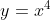 or
or 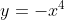 near their quadruple roots at the origin.
near their quadruple roots at the origin.
- Which of these two quartics
) resembles can be determined either by considering the concavity at
resembles can be determined either by considering the concavity at  (concave up resembles
(concave up resembles 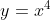 , whereas concave down resembles
, whereas concave down resembles 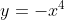 ) or by looking at the sign of
) or by looking at the sign of ) around the root (if
around the root (if ) follows the pattern negative - zero - negative around
follows the pattern negative - zero - negative around  , it resembles
, it resembles 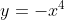 ; if
; if ) follows the pattern positive - zero - positive around
follows the pattern positive - zero - positive around  , it resembles
, it resembles 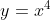 )
)
- The same reasoning / approach applies to the values of
 , governing the behaviour around
, governing the behaviour around 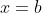 , and to the behaviour around
, and to the behaviour around 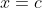 that occurs with different values of
that occurs with different values of 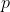 .
.
So, for example, a curve like
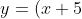^3(x+1)^3(x-2)^4(x-5)(x-7)^2(x-10)^3)
(which is certainly more complicated than would be expected in Advanced Maths) will have:
- a triple root at
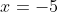
a triple root at
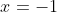
a quadruple root at
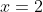
a single root at
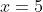
a double root at
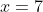
a triple root at
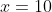
Since the function will have a positive value for sufficiently large

(as every factor will be positive), it will be
- positive for
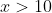
- zero at
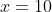 , and, since this a triple root and sign changes at odd-power roots
, and, since this a triple root and sign changes at odd-power roots
- negative for
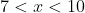
- zero at
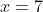 , and, since this a double root and sign does not change at even-power roots
, and, since this a double root and sign does not change at even-power roots
- negative for
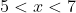
- zero at
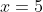 , and, since this a single root and sign changes at odd-power roots
, and, since this a single root and sign changes at odd-power roots
- positive for
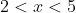
- zero at
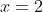 , and, since this a quadruple root and sign does not change at even-power roots
, and, since this a quadruple root and sign does not change at even-power roots
- positive for
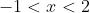 - note, at
- note, at 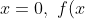 = (5)^3(1)^3(-2)^4(-5)(-7)^2(-10)^3 = 125 \times 1 \times 16 \times -5 \times 49 \times -1000 > 0) , so the
, so the  -intercept is positive, as expected
-intercept is positive, as expected
- zero at
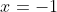 , and, since this a triple root and sign changes at odd-power roots
, and, since this a triple root and sign changes at odd-power roots
- negative for
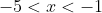
- zero at
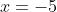 , and, since this a triple root and sign changes at odd-power roots
, and, since this a triple root and sign changes at odd-power roots
- positive for
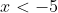
In appearance,
- the root at
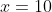 resembles the root of
resembles the root of 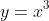 at the origin
at the origin
- the root at
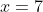 resembles the root of
resembles the root of 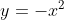 at the origin
at the origin
- the root at
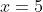 resembles the root of
resembles the root of 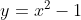 at
at 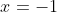 (in that, in the immediate region around the root,
(in that, in the immediate region around the root, ) is positive for
is positive for  -values below the root and negative for for
-values below the root and negative for for  -values above the root), or even more similarly (in that it also matches the concavity being down at the root
-values above the root), or even more similarly (in that it also matches the concavity being down at the root 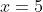 ), the root of
), the root of 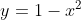 at
at 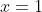
- the root at
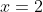 resembles the root of
resembles the root of 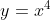 at the origin
at the origin
- the root at
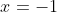 resembles the root of
resembles the root of 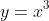 at the origin
at the origin
- the root at
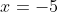 resembles the root of
resembles the root of 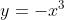 at the origin
at the origin
Now, if you try the Desmos Calculator at
https://www.desmos.com/calculator, you can explore these concepts.
As an example, attached is a graph of
^3x^3(x-2)^4(2x-7)(x-4)(x-5)^2(x-6)^3}{250\ 000})
The factor of 250,000 is to make the

-scale reasonable. You can see the distinctive horizontal point of inflexion shapes of the triple roots at
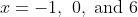
. You can see that the quadruple root at
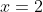
has a much broader / flatter shape around the root than does the double root at
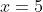
. You can see the single roots at
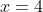
and
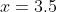
look like the roots / intercepts of a parabola.
