This i have a problem with. I was taught to multiply by (x+y)^2 when the x is in the denominator. So for this question of absolutes
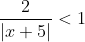
The solutions for this, did not require multiplying denomnator by (x+5)^2, but rather took 2 cases. I was wondering what the rules for this is?
The solutions for this, did not require multiplying denomnator by (x+5)^2, but rather took 2 cases. I was wondering what the rules for this is?
