asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,225
- Gender
- Undisclosed
- HSC
- 2012
We have all seen 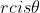 ...and I have also seen it in the Boardofstudies answers.
...and I have also seen it in the Boardofstudies answers.
My teacher said its not in the syallbus so we should stick to) ...but it's obviously a tedious bore to write it all the time.
...but it's obviously a tedious bore to write it all the time.
We are allowed to use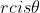 in HSC, yes? I don't want to write
in HSC, yes? I don't want to write ) all the time unless I must.
all the time unless I must.
My teacher said its not in the syallbus so we should stick to
We are allowed to use
