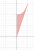
Q20.
c) i: I got wrong, and I disagree with the working out of the solutions book.
ii: I couldn't solve this, and I disagree with the working out of the solutions book.
Just posting this here to see what you guys can do with it Probably an oversight by me; but nonetheless, your help is appreciated.
Probably an oversight by me; but nonetheless, your help is appreciated.
c) i: I got wrong, and I disagree with the working out of the solutions book.
ii: I couldn't solve this, and I disagree with the working out of the solutions book.
Just posting this here to see what you guys can do with it
Attachments
-
278.4 KB Views: 37