Hi there!
Perhaps the best way to start a question like this is to see if you can picture the graph of the functions in your head (or draw them). This will give you a better idea of what's going on. If you can't, use this function plotter:
http://www.univie.ac.at/future.media/moe/fplotter/fplotter.html
Ok. So picture in your head the shells. We're rotating about the line
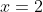
, so clearly these shells are going to have a radius of
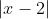
.
In the region
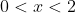
, we know that
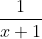
is going to be larger than
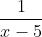
(because the second function is negative!).
Therefore, the height of these shells is
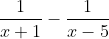
.
And that's it! The volume of the little shells going to be:
|x-2|dx)
Hence the volume is just
(2-x)dx)
Why
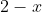
? Because in the region of integration,
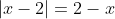
.
Hope this helps!
Rob