HSC Mathematics Marathon (1 Viewer)
- Thread starter ohexploitable
- Start date
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
I go to sydney grammar
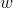 . Then taking the derivative, the following two are true:
. Then taking the derivative, the following two are true:
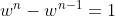
w^{n-2} = 0)
Note eqn (1) implies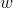 is nonzero. From that we can divide by
is nonzero. From that we can divide by 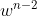 in (2) to obtain:
in (2) to obtain:
 = 0)
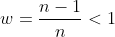
Now the problem with this is that if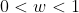 , then
, then 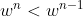 which clearly contradicts the first equation. So it mustn't have had a repeated root in the first place. (messy question)
which clearly contradicts the first equation. So it mustn't have had a repeated root in the first place. (messy question)
Here's a hard integration. Prove:
}{1+x^2} dx = \frac{1}{8} \pi ln2)
Suppose it had a repeated rootim havin a go at largarithmic's question but here's another one in the mean time:
show that the polynomial:
wherecannot have a repeated real root.
Note eqn (1) implies
Now the problem with this is that if
Here's a hard integration. Prove:
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
yeah I initially forgot to end with [ /tex]
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
120wat did u get for ur trial?
apollo1
Banned
- Joined
- Sep 19, 2011
- Messages
- 938
- Gender
- Male
- HSC
- 2011
holy shit. i no whos gonna come first in the state for 4U this year. how about 3U wat did u get for that?
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
highly doubt ill come first, the grammar paper was really nice on me in particular and the markers were nice with some random oddities. got 83/84 for 3uholy shit. i no whos gonna come first in the state for 4U this year. how about 3U wat did u get for that?
apollo1
Banned
- Joined
- Sep 19, 2011
- Messages
- 938
- Gender
- Male
- HSC
- 2011
m8 im willing to bet my life savings that you will come first.highly doubt ill come first, the grammar paper was really nice on me in particular and the markers were nice with some random oddities. got 83/84 for 3u
- Joined
- Feb 16, 2005
- Messages
- 8,402
- Gender
- Male
- HSC
- 2006
Make the substitution x = tan u and then use the properties of definite integrals. I'll let someone else do it in full...
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
pretty poor bet lol. try horses instead. thanks for the encouragement thoughm8 im willing to bet my life savings that you will come first.
yeah thats right, its a bit of a joke problem in a way coz its a bit unmotivatable after you do the trig sub (the usual neat solutions teachers have for it are just like, try this, magic it works). once youve done the trig sub you can do some other neat stuff though that is a bit more motivatable I think like use auxiliary angles but thats still hardTrebla said:Make the substitution x = tan u and then use the properties of definite integrals. I'll let someone else do it in full...
anyway time for a legitimate problem, but keep trying that polynomial thing. try this circle geo its neat
ABC is a triangle, and points D, E, F are chosen arbitrarily on each of sides BC, AC, AB. Let the circle through B,D,F meet the circle through C,D,E at G. Show the circle through A,E,F also goes through G
apollo1
Banned
- Joined
- Sep 19, 2011
- Messages
- 938
- Gender
- Male
- HSC
- 2011
cool it workedMake the substitution x = tan u and then use the properties of definite integrals. I'll let someone else do it in full...
What Trebla said and in addition Put cos theta + sin theta in the form R cos alpha and then using the symmtery property (ie. integral from 0 to a f(x) = integral from 0 to a f(a-x)) and then use log laws.
Btw, where did you get that question from?
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
yeah thatWhat Trebla said and in addition Put cos theta + sin theta in the form R cos alpha and then using the symmtery property (ie. integral from 0 to a f(x) = integral from 0 to a f(a-x)) and then use log laws.
Btw, where did you get that question from?
um it was in my 4u textbook. sydney grammar has its own textbook/handout that it hands out for 4u, apparently all the commercially available ones are crappy. They used to do that for 3u as well, until it got turned into the cambridge 3u book (pender, sadler, shea, ward are all current/former grammar teachers)
They're not "crappy". They're just a bit irrelevant sometimes... Yeah if I was teaching 4U then I'd do that too.apparently all the commercially available ones are crappy.
K4M1N3
Member
- Joined
- Jun 7, 2010
- Messages
- 177
- Gender
- Male
- HSC
- 2011
ABC is a triangle, and points D, E, F are chosen arbitrarily on each of sides BC, AC, AB. Let the circle through B,D,F meet the circle through C,D,E at G. Show the circle through A,E,F also goes through G
However since EGDC is a cyclic quad
Similiarly for BDGF
Subbing 3 and 4 into 2
but from (1)
therefore
ie. angle egf and angle cab are supplmentary
therefore AEGF is a cyclic quad therefore the circle through A E and F must pass through G.
XD
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
"Sydney Grammar School, Mathematics Department, Extension 2 Exercises, 2011, Book One/Two". It's not even a real textbook, its a cheaply printed volume of notes and exercises with a light blue/light green (for book1/book2) cardboard cover.What is it called ?
And I think grammar thought the other textbooks were not challenging enough and didnt teach some of the topics in the way grammar wants to teach them. I dunn othough since Ive never used one
Thats right ^^ its a pretty neat result too, it's called "pivot theorem".(1) (interior angle sum of triangle)
(2) (Angle sum at a point)
However since EGDC is a cyclic quad
(3)
Similiarly for BDGF
(4)
Subbing 3 and 4 into 2
but from (1)
therefore
ie. angle egf and angle cab are supplmentary
therefore AEGF is a cyclic quad therefore the circle through A E and F must pass through G.
XD
Anyway try this really nice probability question.
Alice and Bob take turns flipping a coin. Alice flips the coin N+1 times, and Bob flips it N times, where N is a positive integer. Alice 'wins' if she gets strictly more heads than Bob does. (e.g. if N=5 and Alice gets 4 heads 2 tails, while Bob gets 3 heads 2 tails, Alice wins; whereas if Bob got 4 heads 1 tail, she doesnt; and if he got all heads, he doesn't). Find the probability that Alice wins (in terms of N if necessary).
Last edited:
