bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,509
- Gender
- Male
- HSC
- 2013
how would you go about q2 d?
not to mention u did the wrong question :L<a href="http://www.codecogs.com/eqnedit.php?latex=$Let $a@plus;ib=\sqrt{21-20i}\\ \therefore (a@plus;ib)^2=a^2@plus;2abi-b^2=21-20i\\ ~\\ $Equating Real and Imaginary parts we get$\\ a^2-b^2=21~~~~~~~~(1)\\ 2ab=-20\\ ab=-10\\ b=-\frac{10}{a}~~~~~~~~~~~~~~~~(2)\\ ~\\ $Subbing (2) into (1):$\\ a^2-\frac{100}{a^2}=21 a^4-21a^2-100=0\\ a^2=\frac{21 \pm \sqrt{21^2@plus;4\cdot 100}}{2}=\frac{21\pm 29}{2}=25 (Since a is real)\\ \therefore a=\pm 5\\ b=\frac{-10}{5}=-2\\ \\ $Hence $\sqrt{21-20i}=\pm(5-2i)" target="_blank"><img src="http://latex.codecogs.com/gif.latex?$Let $a+ib=\sqrt{21-20i}\\ \therefore (a+ib)^2=a^2+2abi-b^2=21-20i\\ ~\\ $Equating Real and Imaginary parts we get$\\ a^2-b^2=21~~~~~~~~(1)\\ 2ab=-20\\ ab=-10\\ b=-\frac{10}{a}~~~~~~~~~~~~~~~~(2)\\ ~\\ $Subbing (2) into (1):$\\ a^2-\frac{100}{a^2}=21 a^4-21a^2-100=0\\ a^2=\frac{21 \pm \sqrt{21^2+4\cdot 100}}{2}=\frac{21\pm 29}{2}=25 (Since a is real)\\ \therefore a=\pm 5\\ b=\frac{-10}{5}=-2\\ \\ $Hence $\sqrt{21-20i}=\pm(5-2i)" title="$Let $a+ib=\sqrt{21-20i}\\ \therefore (a+ib)^2=a^2+2abi-b^2=21-20i\\ ~\\ $Equating Real and Imaginary parts we get$\\ a^2-b^2=21~~~~~~~~(1)\\ 2ab=-20\\ ab=-10\\ b=-\frac{10}{a}~~~~~~~~~~~~~~~~(2)\\ ~\\ $Subbing (2) into (1):$\\ a^2-\frac{100}{a^2}=21 a^4-21a^2-100=0\\ a^2=\frac{21 \pm \sqrt{21^2+4\cdot 100}}{2}=\frac{21\pm 29}{2}=25 (Since a is real)\\ \therefore a=\pm 5\\ b=\frac{-10}{5}=-2\\ \\ $Hence $\sqrt{21-20i}=\pm(5-2i)" /></a>
After typing this all out I realised that there's worked solutions at the end of that paper.
this stems from the fact thatBasically just mutliply the vector z1a by i to rotate it 90 degrees:
<a href="http://www.codecogs.com/eqnedit.php?latex=(i)(z_{1}-a)=(z_{2}-a)\\ iz_{1}-ai=z_{2}-a \\z_{2}=a(1-i)@plus;iz_{1}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?(i)(z_{1}-a)=(z_{2}-a)\\ iz_{1}-ai=z_{2}-a \\z_{2}=a(1-i)+iz_{1}" title="(i)(z_{1}-a)=(z_{2}-a)\\ iz_{1}-ai=z_{2}-a \\z_{2}=a(1-i)+iz_{1}" /></a>
Good God, I can not believe I didn't realise that...thanks.Basically just mutliply the vector z1a by i to rotate it 90 degrees:
<a href="http://www.codecogs.com/eqnedit.php?latex=(i)(z_{1}-a)=(z_{2}-a)\\ iz_{1}-ai=z_{2}-a \\z_{2}=a(1-i)@plus;iz_{1}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?(i)(z_{1}-a)=(z_{2}-a)\\ iz_{1}-ai=z_{2}-a \\z_{2}=a(1-i)+iz_{1}" title="(i)(z_{1}-a)=(z_{2}-a)\\ iz_{1}-ai=z_{2}-a \\z_{2}=a(1-i)+iz_{1}" /></a>
I thought you weren't allowed to combine vector notation with complex numbers..not to mention u did the wrong question :L
this stems from the fact that
<a href="http://www.codecogs.com/eqnedit.php?latex=\overrightarrow{AZ_1}=Z_1-A\\$and $ \overrightarrow{AZ_2}=Z_2-A" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\overrightarrow{AZ_1}=Z_1-A\\$and $ \overrightarrow{AZ_2}=Z_2-A" title="\overrightarrow{AZ_1}=Z_1-A\\$and $ \overrightarrow{AZ_2}=Z_2-A" /></a>
I thought you weren't allowed to combine vector notation with complex numbers..
lol that's not what i meant. For e.g.where did u hear that from? all of terry lee's worked examples and solutions in geometrical applications of complex numbers use vector notation
lol that's not what i meant. For e.g.
or
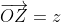
I'm not sure why, it's just what my tutor instilled in meis what im talking about; is that wat u mean by combining vector notation with complex numbers? when u say 'not allowed', do u mean not board approved or your not allowed because it wont work?
bad tutor is bad,I'm not sure why, it's just what my tutor instilled in me
