Math help (2 Viewers)
- Thread starter Fawun
- Start date
Re: Math help (Because Carrot made me do this)
So you have the intercepts where they are both 0
You have the vertical asymptote by making the denominator = 0
You have the horizontal asymptote by doing the limits
Do we just sub large numbers in like how Sy explained before?
Also, how do you know when to use limits?
Okay so what happens next?Yes, the horizontal asymptote.
Divide by the highest power of x.
So you have the intercepts where they are both 0
You have the vertical asymptote by making the denominator = 0
You have the horizontal asymptote by doing the limits
Do we just sub large numbers in like how Sy explained before?
Also, how do you know when to use limits?
Re: Math help (Because Carrot made me do this)
So how would I go in doing this question? I'm stuck :s

This is all I have so far:
 = \frac{x^2}{x-2})
 = \frac{(-x)^2}{(-x)-2})


Which is neither an even or an odd function.
x-intercept:


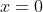
y-intercept:

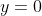
vertical asymptote:


horizontal asymptote:




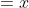
But I don't get it. How can x (which is infinity) be the horizontal asymptote?
So how would I go in doing this question? I'm stuck :s
This is all I have so far:
Which is neither an even or an odd function.
x-intercept:
y-intercept:
vertical asymptote:
horizontal asymptote:
But I don't get it. How can x (which is infinity) be the horizontal asymptote?
Re: Math help (Because Carrot made me do this)
Where are you up to?@Fawun - I haven't even gotten to limits yet. So far ahead...
Timske
Sequential
- Joined
- Nov 23, 2011
- Messages
- 794
- Gender
- Male
- HSC
- 2012
- Uni Grad
- 2016
Re: Math help (Because Carrot made me do this)
so ur horizontal asymp. is y= 0
0/1-0 = 0So how would I go in doing this question? I'm stuck :s
This is all I have so far:
Which is neither an even or an odd function.
x-intercept:
y-intercept:
vertical asymptote:
horizontal asymptote:

But I don't get it. How can x (which is infinity) be the horizontal asymptote?
so ur horizontal asymp. is y= 0
Re: Math help (Because Carrot made me do this)
How can it be 0 if our intercepts are at (0,0)?0/1-0 = 0
so ur horizontal asymp. is y= 0
Timske
Sequential
- Joined
- Nov 23, 2011
- Messages
- 794
- Gender
- Male
- HSC
- 2012
- Uni Grad
- 2016
Re: Math help (Because Carrot made me do this)
asymptotes can cross interceptsHow can it be 0 if our intercepts are at (0,0)?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Im bored with English at the moment, so I will mention what limits are:
Take my analogy for instance:
I am in an unknown world and galaxy, and I set off on a road to a distant town, I can always see the town in the horizon, yet when I keep going closer, and closer but I can never ever quite get to it. Its there and I know its there, I can even see it, but I keep going closer and I cant make it...
We can say that throughout my whole journey, the limit of my journey was the town, that is its the limiting destination, it limits me from going any further. Think of it as though its some sort of boundary.
A limit is hence our 'boundary', or the limit in what we can do.
Take a fundemental limit:

What this means is that, the limit of our function is 0. We can never be 0, yet we can be everything else. We cant be 0 and hence its our limiting value at infinity
Be careful when you say
Because infinity inst a number. But for simplicity purposes you can see it like that.
How does this relate to asymptotes?
Well, we need to first define what asymptotes are, they are lines (or in further maths they can be curves but dont worry about that for now), they are lines which a function will approach at any infinity.
What I mean by any infinity is, that if we approach say, y=3 at an x-infinite, then there is an asymptote at y=3 (its horizontal because y=3 is horizontal)
If we approach x=2 at a y-infinite, then we have a vertical asymptote at x=2 etc.
What limits allow us to do, is to find these asymptotes, because asymptotes 'limit' us. We need to find the limiting value of something by well taking the limit of it.
Say we want to find the limiting value of
=\frac{3x}{2x-1} )
We want to find where the function approaches, or its limiting value at infinity, so lets take the limit of it:

You know how to evaluate them, just divide everything by the highest power
the answer should be 3/2.
(If you notice according to that 'formula' I told you about for finding asymptotes, it fits as you can see and it follows the same principle to derive it)
Our horizontal asymptote then is y=3/2
Nag your tutor to teach you what they really are.
Or get a new one
One more thing, certain graphs CAN cross horizontal asymptotes, this is possible. BUT NO GRAPH, can ever cross vertical asymptotes (if they can disastrous things will happen). If the trajectory of the curve makes it so that you have to 'cross' a vertical asymptote, then just put an open circle there. (This is more advanced though, you may not need to know it but I dont know the y10 syllabus all that well)
Also if my idea of concept of the limit is wrong, then I have made myself one heck of a fool on here
Take my analogy for instance:
I am in an unknown world and galaxy, and I set off on a road to a distant town, I can always see the town in the horizon, yet when I keep going closer, and closer but I can never ever quite get to it. Its there and I know its there, I can even see it, but I keep going closer and I cant make it...
We can say that throughout my whole journey, the limit of my journey was the town, that is its the limiting destination, it limits me from going any further. Think of it as though its some sort of boundary.
A limit is hence our 'boundary', or the limit in what we can do.
Take a fundemental limit:
What this means is that, the limit of our function is 0. We can never be 0, yet we can be everything else. We cant be 0 and hence its our limiting value at infinity
Be careful when you say
Because infinity inst a number. But for simplicity purposes you can see it like that.
How does this relate to asymptotes?
Well, we need to first define what asymptotes are, they are lines (or in further maths they can be curves but dont worry about that for now), they are lines which a function will approach at any infinity.
What I mean by any infinity is, that if we approach say, y=3 at an x-infinite, then there is an asymptote at y=3 (its horizontal because y=3 is horizontal)
If we approach x=2 at a y-infinite, then we have a vertical asymptote at x=2 etc.
What limits allow us to do, is to find these asymptotes, because asymptotes 'limit' us. We need to find the limiting value of something by well taking the limit of it.
Say we want to find the limiting value of
We want to find where the function approaches, or its limiting value at infinity, so lets take the limit of it:
You know how to evaluate them, just divide everything by the highest power
the answer should be 3/2.
(If you notice according to that 'formula' I told you about for finding asymptotes, it fits as you can see and it follows the same principle to derive it)
Our horizontal asymptote then is y=3/2
Nag your tutor to teach you what they really are.
Or get a new one
One more thing, certain graphs CAN cross horizontal asymptotes, this is possible. BUT NO GRAPH, can ever cross vertical asymptotes (if they can disastrous things will happen). If the trajectory of the curve makes it so that you have to 'cross' a vertical asymptote, then just put an open circle there. (This is more advanced though, you may not need to know it but I dont know the y10 syllabus all that well)
Also if my idea of concept of the limit is wrong, then I have made myself one heck of a fool on here
Last edited:
Re: Math help (Because Carrot made me do this)
I've finished the year 10 topics for maths with my tutor. I don't really accelerate that far ahead to be honest.Where are you up to?
JINOUGA
Member
Re: Math help (Because Carrot made me do this)
but its x/(1-0)
and as x is approaching infinity, doesn't that mean there is no horizontal asymptote?
?0/1-0 = 0
so ur horizontal asymp. is y= 0
but its x/(1-0)
and as x is approaching infinity, doesn't that mean there is no horizontal asymptote?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: Math help (Because Carrot made me do this)
That is the inclined asymptote, which is y=x in this case
You must use polynomial division in this case. Ill get on this indepth later
Where did you get this question? Tutor or book? Finding the asymptote to this one is harder because it introduces a slant asymptote.So how would I go in doing this question? I'm stuck :s
This is all I have so far:
Which is neither an even or an odd function.
x-intercept:
y-intercept:
vertical asymptote:
horizontal asymptote:

But I don't get it. How can x (which is infinity) be the horizontal asymptote?
That is the inclined asymptote, which is y=x in this case
You must use polynomial division in this case. Ill get on this indepth later
Re: Math help (Because Carrot made me do this)
I know how to do polynomial division (the one that you learn in year 10 right? as the optional topics? and to just to save you some time from explaining it) but what is there to divide?
So kind of like a rainbow right?Im bored with English at the moment, so I will mention what limits are:
Take my analogy for instance:
I am in an unknown world and galaxy, and I set off on a road to a distant town, I can always see the town in the horizon, yet when I keep going closer, and closer but I can never ever quite get to it. Its there and I know its there, I can even see it, but I keep going closer and I cant make it...
We can say that throughout my whole journey, the limit of my journey was the town, that is its the limiting destination, it limits me from going any further. Think of it as though its some sort of boundary.
Yeah i'm trying to. I have to stay with my tutor for another month or so though. So until then, I have to put up with her teaching ways. I can't really ask questions though because all the selective kids give me these 'how can you not know this' types of looks so it's kind of embarrassing.Nag your tutor to teach you what they really are.
Or get a new one
What do you mean cross horizontal asymptotes? As in go through it? touch it? or?One more thing, certain graphs CAN cross horizontal asymptotes, this is possible. BUT NO GRAPH, can ever cross vertical asymptotes (if they can disastrous things will happen). If the trajectory of the curve makes it so that you have to 'cross' a vertical asymptote, then just put an open circle there. (This is more advanced though, you may not need to know it but I dont know the y10 syllabus all that well)
I got this question from my tutor. She wrote it on the board and I had to quickly copy it down before she moved on to the next question.Where did you get this question? Tutor or book? Finding the asymptote to this one is harder because it introduces a slant asymptote.
That is the inclined asymptote, which is y=x in this case
You must use polynomial division in this case. Ill get on this indepth later
I know how to do polynomial division (the one that you learn in year 10 right? as the optional topics? and to just to save you some time from explaining it) but what is there to divide?
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,423
- Gender
- Male
- HSC
- N/A
Re: Math help (Because Carrot made me do this)
Without involving a direct polynomial long division, you can manipulate it so you can see the oblique asymptote:
+4}{x-2}\\\\=\frac{(x^2-4)}{x-2}+\frac{4}{x-2}\\\\=\frac{(x-2)(x+2)}{x-2}+\frac{4}{x-2}\\\\=\(x+2)+\frac{4}{x-2}\\\\)
So then the oblique asymptote is the asymptote described by the line y = x-2. Something which you probably would not have covered.
This part is "not totally correct". You divide by the highest power of x, so in this example, the higher power is a square power, so you divide top and bottom by x2. However, this question contains something which is covered in MX2 - oblique/slanted asymptote, where the asymptote is at an angle (i.e. not horizontal nor vertical).horizontal asymptote:

But I don't get it. How can x (which is infinity) be the horizontal asymptote?
Without involving a direct polynomial long division, you can manipulate it so you can see the oblique asymptote:
So then the oblique asymptote is the asymptote described by the line y = x-2. Something which you probably would not have covered.
Last edited:
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,423
- Gender
- Male
- HSC
- N/A
Re: Math help (Because Carrot made me do this)
So, since the power of x2 (numerator) is larger than the power of x-2 (denominator), you can apply a polynomial long division.
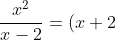+\frac{4}{x-2}\\\\)
If you have 3x2/x, that can be simplified to 3x. What you're doing is dividing. In these simple cases, if the largest power of polynomial on the numerator is larger than the largest power of the polynomial on the denominator, then it can be usually simplified, or, divided.I know how to do polynomial division (the one that you learn in year 10 right? as the optional topics? and to just to save you some time from explaining it) but what is there to divide?
So, since the power of x2 (numerator) is larger than the power of x-2 (denominator), you can apply a polynomial long division.
Re: Math help (Because Carrot made me do this)
But first you had:

Then you had:

Where did you get the x^2-4+4 from?
Also, thanks for helping
So I divide (x-2) into x^2?If you have 3x2/x, that can be simplified to 3x. What you're doing is dividing. In these simple cases, if the largest power of polynomial on the numerator is larger than the largest power of the polynomial on the denominator, then it can be usually simplified, or, divided.
So, since the power of x2 (numerator) is larger than the power of x-2 (denominator), you can apply a polynomial long division.
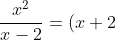+\frac{4}{x-2}\\\\)
Lol that means that my tutor did her working out wrong then :sThis part is wrong. You divide by the highest power of x, so in this example, the higher power is a square power, so you divide top and bottom by x2. However, this question contains something which is covered in MX2 - oblique/slanted asymptote, where the asymptote is at an angle (i.e. not horizontal nor vertical).
Without involving a direct polynomial long division, you can manipulate it so you can see the oblique asymptote:
So then the oblique asymptote is the asymptote described by the line y = x-2. Something which you probably would not have covered.
But first you had:
Then you had:
Where did you get the x^2-4+4 from?
Also, thanks for helping
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,423
- Gender
- Male
- HSC
- N/A
Re: Math help (Because Carrot made me do this)
So we can see the denominator has x-2, so it's right there in your face telling you that if we have x2-4, we can simplify that to x+2. But if we minus 4, we must add 4 to make it balanced, so we add 4 and then we can split up the polynomial into the (x+2) and 4/(x-2) terms.
Yes, for that question.So I divide (x-2) into x^2?
Actually, after re-reading it, it's not totally wrong, but it's not good mathematics. We never say the limit of something is infinity because infinity is not a number.Lol that means that my tutor did her working out wrong then :s
What is -4 + 4? That equals zero, so I haven't changed the value of the equation - it's still the same thing. If you haven't done polynomial long division, then a quick and neat way is to recognise the numerator and denominator can be manipulated such that we get a simpler form or a split up form.But first you had:
Then you had:
Where did you get the x^2-4+4 from?
Also, thanks for helping
So we can see the denominator has x-2, so it's right there in your face telling you that if we have x2-4, we can simplify that to x+2. But if we minus 4, we must add 4 to make it balanced, so we add 4 and then we can split up the polynomial into the (x+2) and 4/(x-2) terms.
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: Math help (Because Carrot made me do this)
You can just do normal polynomial division of x-2 by x^2, the thing you get ontop is your oblique asymptote, (ignore the remainder).
Also I dont get what you mean by limits are like a Rainbow?
Also when I mean they can cross horizontal asymptotes, it means they can pass over them without restriction, however for it to be an asymptote at on the ends on the graph, it must display the asymptote behaviour and have the function approach it.
D94 was simply displaying a creative technique in simplifying the fraction into a form where we can get our slant asymptote.So I divide (x-2) into x^2?
Lol that means that my tutor did her working out wrong then :s
But first you had:
Then you had:
Where did you get the x^2-4+4 from?
Also, thanks for helping
You can just do normal polynomial division of x-2 by x^2, the thing you get ontop is your oblique asymptote, (ignore the remainder).
Also I dont get what you mean by limits are like a Rainbow?
Also when I mean they can cross horizontal asymptotes, it means they can pass over them without restriction, however for it to be an asymptote at on the ends on the graph, it must display the asymptote behaviour and have the function approach it.
Re: Math help (Because Carrot made me do this)
How do you do that?
lolwut
If you haven't done polynomial long division, then a quick and neat way is to recognise the numerator and denominator can be manipulated such that we get a simpler form or a split up form.
How do you do that?
So we can see the denominator has x-2, so it's right there in your face telling you that if we have x2-4, we can simplify that to x+2. But if we minus 4, we must add 4 to make it balanced, so we add 4 and then we can split up the polynomial into the (x+2) and 4/(x-2) terms.
lolwut
How do you know WHEN to use polynomial division?You can just do normal polynomial division of x-2 by x^2, the thing you get ontop is your oblique asymptote, (ignore the remainder).
So it's like a rainbow right? because you can see a rainbow but you can never 'touch' it or something.Also I dont get what you mean by limits are like a Rainbow?
what's that? :sAlso when I mean they can cross horizontal asymptotes, it means they can pass over them without restriction, however for it to be an asymptote at on the ends on the graph, it must display the asymptote behaviour and have the function approach it.
