His methods a lot better than long division and more efficient when one gets used to the equating co-effs poly method.Or you could use long division...
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Imaginay Nos (1 Viewer)
- Thread starter Lukybear
- Start date
"Better" is a subjective term.His methods a lot better than long division and more efficient when one gets used to the equating co-effs poly method.
Personally, I'd prefer to use long division. But I was just pointing out that there is an alternative method.
Also this question:

. Show that as the point z describes the y axis, from the negative end to the positive end, the point Z (upper case) describes completely the circle x^2+y^2=1, in the coutner-clockwise sense.
Ive got x^2+y^2=4 as the circle, and not the question stated x^2+y^2=1. Can anyone confirm?
. Show that as the point z describes the y axis, from the negative end to the positive end, the point Z (upper case) describes completely the circle x^2+y^2=1, in the coutner-clockwise sense.
Ive got x^2+y^2=4 as the circle, and not the question stated x^2+y^2=1. Can anyone confirm?
Look in the Coroneos 4U book. It's there in one of the examples.How is long divison achieved? Could you show via a eaxmple?
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
Also this question:
. Show that as the point z describes the y axis, from the negative end to the positive end, the point Z (upper case) describes completely the circle x^2+y^2=1, in the coutner-clockwise sense.
Ive got x^2+y^2=4 as the circle, and not the question stated x^2+y^2=1. Can anyone confirm?
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
Also this question.
Prove that if z lies on the circle x^2+y^2=1, the points representing
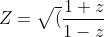)
lies on an orthogonal line pair.
not 100% sure how to proceed
K
khorne
Guest
Where are you even getting these questions from? They don't look very standard to me.
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
One more:
If P, Q represent the complex no.s z, Z and
find the locus of Q as P moves on the circle |z-3|=3
not sure if this correct
Last edited:
- Joined
- Feb 16, 2005
- Messages
- 8,403
- Gender
- Male
- HSC
- 2006
LOL, that is a term commonly used for vectors in a number space and matrix algebra...don't think it's that relevant to HSCAlso this question.
Prove that if z lies on the circle x^2+y^2=1, the points representing
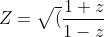)
lies on an orthogonal line pair.
Which chapter? Its not in Imaginary thats a for sure.Look in the Coroneos 4U book. It's there in one of the examples.
reali? I thought it was just y=+-xLOL, that is a term commonly used for vectors in a number space and matrix algebra...don't think it's that relevant to HSC
gurmies
Drover
Orthogonal means at 90 degrees to.

Last edited:
Absolutely rite. Can i just ask, i did it just graphically. I was like: the locus of that was
not sure if this correct
The locus of 1/z-3 was a circle of same centre but with radius 1/3. Hence 1/z-3 + 17/3 equals to a locaus of (x-3-17/3)^2 + y^2 = 1/9
Where did i go wrong with that method?
Yep and y=+-x makes 90 degrees at centre.Orthogonal means at 90 degrees to.
K
khorne
Guest
Wouldn't the radius be the same, but the center be shifted, as 17/3 only shifts it?Absolutely rite. Can i just ask, i did it just graphically. I was like: the locus of that was
The locus of 1/z-3 was a circle of same centre but with radius 1/3. Hence 1/z-3 + 17/3 equals to a locaus of (x-3-17/3)^2 + y^2 = 1/9
Where did i go wrong with that method?
So how would one determine the shifted centre?Wouldn't the radius be the same, but the center be shifted, as 17/3 only shifts it?
K
khorne
Guest
On additional thought, I think you are right as to say that the radius changes too...So how would one determine the shifted centre?
Which book are these problems from.
Last edited by a moderator:
