After looking at my working I found a big brain substitution:Just a question. The standard way to do this integral seems to look like a page of working at least.
Any short ways?
Which gets you straight to:
After looking at my working I found a big brain substitution:Just a question. The standard way to do this integral seems to look like a page of working at least.
Any short ways?
Finding the antiderivative is very easy using a t-sub. I've shown a different way the antiderivative can be found below:It's not too hard to get the antiderivative in terms of elementary function...but the evil is in the substitution of upper and lower limits.
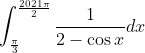
Ok, thanks for the insight!Periodicity is not the cause of this trouble. If you integrate cos x, then you get sin x which is periodic. However, the substitution still works as usual.
The cause of this trouble is a different constant of integration at different intervals.
Instead of +c for all real numbers, you actually have +c0 for -pi<=x<=pi, +c1 for pi<=x<=3pi, +c2 for 3pi<=x<=5pi, etc.
Actually, the functionPeriodicity is not the cause of this trouble. If you integrate cos x, then you get sin x which is periodic. However, the substitution still works as usual.
The cause of this trouble is a different constant of integration at different intervals.
Instead of +c for all real numbers, you actually have +c0 for -pi<=x<=pi, +c1 for pi<=x<=3pi, +c2 for 3pi<=x<=5pi, etc.
This is the 2021 integration marathon thread, as i have noticed users submitting integrals on previous year's threads.
I will start off:
1/(x+x^6)
sorry for bad formatting
Let
Show all necessary working, please. V tricky.
Couldn't have asked for moreLet
where C is a constant
where
is another constant
Same adding and subtracting the same thing trick as the previous question:Try:
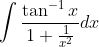
let x = tan uTry:
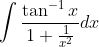
this method is more intuitive and quicker I reckon esp if you know what the integral of inverse tan is off by heart.Same adding and subtracting the same thing trick as the previous question:
IBP on the first integral gives:
Second integral is just reverse chain rule
So in total: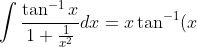-\frac{1}{2}\ln(x^2+1)-\frac{1}{2} (\tan^{-1}(x))^2+C_1)
This was the intended method.this method is more intuitive and quicker I reckon esp if you know what the integral of inverse tan is off by heart.
