HSC 2012 MX2 Marathon (archive) (2 Viewers)
- Thread starter nightweaver066
- Start date
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Other attempts pl0x. I like this question.
Some Conics...
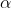\; $Let$\; a\;$ and $\;b \;$ be positive constants.$)
.
 Find the area of the region bounded by $\;E_{1} \;, \; E_{2} \; $and$ \; L.\; \; \; \fbox{2})
You can do it.For part alpha I can't work out why m<0. I can see it must be the case for the rest of the question because of the domain.
Other attempts pl0x. I like this question.
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,044
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
 )
)
I enjoyed the question too - I did the rest of it last night after skipping the first part (which I still can't getYou can do it.
Other attempts pl0x. I like this question.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Use the force.
Use the force.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Let the discriminant be equal to zero and after a whole lot of algebra, you should get the solution.
However, I do not understand why m < 0 is a condition. I do not see why positive gradients are excluded as possible tangents.
This is only the case if we purely consider the first quadrant of the Ellipse in canonical form and the equation you provided covers the first 2 quadrants.
Substitute y=mx+c into the equation of the semi-ellipse and make a quadratic in terms of x.I did the rest of it last night after skipping the first part (which I still can't get)
Let the discriminant be equal to zero and after a whole lot of algebra, you should get the solution.
However, I do not understand why m < 0 is a condition. I do not see why positive gradients are excluded as possible tangents.
This is only the case if we purely consider the first quadrant of the Ellipse in canonical form and the equation you provided covers the first 2 quadrants.
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,044
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
That's exactly what I was struggling with (why m<0), I got the rest of it, I just assumed I was missing something since Spiral's almost always correct and nobody else had mentioned anything.Substitute y=mx+c into the equation of the semi-ellipse and make a quadratic in terms of x.
Let the discriminant be equal to zero and after a whole lot of algebra, you should get the solution.
However, I do not understand why m < 0 is a condition. I do not see why positive gradients are excluded as possible tangents.
This is only the case if we purely consider the first quadrant of the Ellipse in canonical form and the equation you provided covers the first 2 quadrants.
Re: 2012 HSC MX2 Marathon
Lol I'm stuck at this point too, can't work that out.For part alpha I can't work out why m<0.
Last edited:
Re: 2012 HSC MX2 Marathon
The equation of the ellipse is the top semi-ellipse
Covering the first two quadrants. Now when you sub
Y=mx+c into semi ellipse and form a quadratic in x
The y int of the tangent must be positive otherwise
It can't be a tangent to the top semi ellipse so c>0, now
As for m<0 there is only one possible way this can
Occur and that is if the x coordinate of the point of
Contact of the tangent is positive. This is deduced if
You find the x value of the point of contact using
The double root method, and this shows the x value of the
Poiny of contact is positive if m<0 otherwise the x value
Will be negative, so this condition for m can't occur unless
The tangent interests in the first quadrant
The equation of the ellipse is the top semi-ellipse
Covering the first two quadrants. Now when you sub
Y=mx+c into semi ellipse and form a quadratic in x
The y int of the tangent must be positive otherwise
It can't be a tangent to the top semi ellipse so c>0, now
As for m<0 there is only one possible way this can
Occur and that is if the x coordinate of the point of
Contact of the tangent is positive. This is deduced if
You find the x value of the point of contact using
The double root method, and this shows the x value of the
Poiny of contact is positive if m<0 otherwise the x value
Will be negative, so this condition for m can't occur unless
The tangent interests in the first quadrant
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,044
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
MOAR CONICS!!
<a href="http://www.codecogs.com/eqnedit.php?latex=\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}@plus;\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx@plus;c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}@plus;\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}+\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx+c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" title="\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}+\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx+c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" /></a>
MOAR CONICS!!
<a href="http://www.codecogs.com/eqnedit.php?latex=\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}@plus;\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx@plus;c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}@plus;\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}+\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx+c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" title="\\ $(Q1)$\\ $Prove that the pair of tangents from the point $ P(4,5)$ to the ellipse $ \frac{x^2}{25}+\frac{y^2}{16}=1 $ are at right angles to one another$~\\ \\ $(Q2)$\\ $Obtain the quadratic equation satisfied by $m$ where $m$ is the gradient of the tangent $ y=mx+c$ from the external point $P(x_1,y_1)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $. Hence, find the locus of $P$ if the two tangents from $P$ are at right angles.$" /></a>
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Last edited:
OMGITzJustin
Well-Known Member
- Joined
- Jun 28, 2010
- Messages
- 1,002
- Gender
- Male
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
what is the best method of graphing 1/f(x) graphs? for example 1/sinx?
what is the best method of graphing 1/f(x) graphs? for example 1/sinx?
Re: 2012 HSC MX2 Marathon
note when f(x) equals 0 there becomes vertical asymptotes. Also the turning points on f(x) stay the same, only the y value changes
and the type of turning point reverses
f(x) represents the y values and 1/f(x) means 1 over every y value. So you use limits as f(x) appraoches 0 and infinity andwhat is the best method of graphing 1/f(x) graphs? for example 1/sinx?
note when f(x) equals 0 there becomes vertical asymptotes. Also the turning points on f(x) stay the same, only the y value changes
and the type of turning point reverses
- Joined
- Feb 16, 2005
- Messages
- 8,402
- Gender
- Male
- HSC
- 2006
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
Re: 2012 HSC MX2 Marathon
question kinda hints to use GP
Noting that for
for 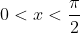 , see that:
, see that:
} dx = \int \frac{\cos x}{1-\sin x} dx=\int \cos x \sum_{n=0}^\infty \sin^n x dx )
Assuming interchangeability between integral and summation, the result follows easily.
question kinda hints to use GP
Noting that
Assuming interchangeability between integral and summation, the result follows easily.

